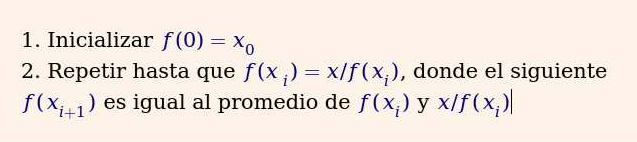Recuerdo cuando en la escuela tuve que memorizar el desarrollo del binomio al cuadrado (a + b) ^2:

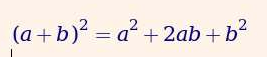
el primer término al cuadrado mas/menos el doble del primero por el segundo, mas el segundo al cuadrado.

Ok. Ahora toca el turno memorizar el desarrollo del binomio al cubo (a + b) ^3:

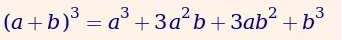
El primer término al cubo, mas 3 veces el primer término al cuadrado por el segundo, mas 3 veces el primer término por el segundo al cuadrado, mas el segundo al cubo.

Ahora, qué tal si se desea que el binomio sea elevado a la n potencia? También tendríamos que memorizar la fórmula?
No, afortunadamente muchos matemáticos han estudiado cómo se comportan estos coeficientes. Y ahora podemos deducir los coeficientes simplemente construyendo lo que se conoce como triángulo de Pascal.

Empezamos en la primera fila con un 1. En la segunda fila creamos dos ramas, con 1 también. A partir de ahora cada número dentro del triángulo es la suma de los dos que están colocados arriba de él.

Olvídate de memorizar porque es más sencillo desarrollar el triángulo de Pascal para la potencia que desemos desarrollar el binomio.

Computación ha sido un tema estudiado mucho antes de la era de las computadoras. Científicos a través de la antigüedad, por muchos siglos, realizaron cálculos para entender sus modelos científicos y matemáticos.

Sin una computadora, esto matemáticos estaban interesados en métodos eficientes porque todos los cálculos eran hechos a mano. Por ejemplo, demos un vistazo al método Newton-Raphson para calcular la raíz cuadrada de x:

f(x) = √x

Ejemplo, para calcular la √2 (hasta una precisión deseada), tenemos los siguientes resultados:

i	f(xi)	2/f(xi)	promedio
0	2	1	1.5
1	1.5	1.3333	1.4166
2	1.4166	1.4117	1.4142

Que tal si nos ayudamos de una computadora para calcular la √2 hasta 15 dígitos? A continuación tenemos el programa en Java para calcular la raíz cuadrada.

public class Sqrt {

	public static void main(String[] args) {
		double epsilon = 1e-15;
		double x = Double.parseDouble(args[0]);
		double squareRoot = x;
		while (Math.abs(squareRoot - x / squareRoot) > epsilon * squareRoot) {
			// Calculate average:
			squareRoot = (x / squareRoot + squareRoot) / 2.0;
			System.out.println(squareRoot);
		}
	}
}

Cuando ejecutamos el programa, obtenemos la raíz de 2 hasta 15 dígitos de precisión.

%java Sqrt 2
1.5
1.4166666666666665
1.4142156862745097
1.4142135623746899
1.414213562373095

Definitivamente es un gran alivio el usar un lenguaje de programación para resolver cálculos matemáticos de manera repetitiva. De igual manera, pudieras utilizar un programa para calcular los dígitos del número π. En 2016 se había logrado calcular hasta 13 billones de cifras decimales. En marzo del 2019 se logró el nuevo record de 31 billones de dígitos. Aquí lo maravilloso es que esos 31 billones de cifras decimales han sido exactamente 31.415.926.535.897 decimales, o lo que es lo mismo, una representación numérica de π con sus primeros 13 decimales!!!

Gracias a las computadoras y los lenguajes de programación utilizamos apps todos los días de manera inadvertida. Te gustaría poder crear tus propias applicaciones?

Aprende a programar ya!